SpikeFun v0.90 - More Complex Pyramidal Neurons, Demo with 3.52 Billion Synapses and more...
Click here to download SpikeFun...
SpikeFun v0.90 has been released today, and with it some important improvements have been made:
Pyramidal Neurons
Let's start with the neuron model - until this version, pyramidal neurons were created as "balls and sticks", where balls were approximations of the soma and "sticks" were approximations of apical dendrites. This approximation was easy to create, but it did not capture some of the interesting phenomena happening inside the real pyramidal neurons, which can have quite complex dendritic tree morphologies and different dendritic regions including apical tufts .
SpikeFun v0.90 brings more complex pyramidal cell morphologies, including:
- Dendritic trees with branching
- Apical tufts
- Basal dendrites in the home cortical layer
Above features are possible when the number of putative synapses is high enough during simulation build-up (1 dendritic compartment holds up to 40 synaptic sites by default, which can be changed in the project configuration XML file). These extended features allow new phenomena, such as dendritic computations, to be simulated with SpikeFun v0.90, which were previously not possible. DigiCortex engine permits dendritic spikes and dendritic STDP, so synapses can be potentiated or depressed regardless of the somatic spikes, as observed in vivo.
For each pyramidal neuron type it is possible to define the extend of axonal and dendritic laminar spreads per cortical layer, which will guide the creation of the actual neuron's morphology. In addition, it is possible to adjust the branching probabilities, which guide the formation of dendritic tree branches. In the future this model will be replaced with the more complex and biologically realistic algorithm based on the wiring conservation.
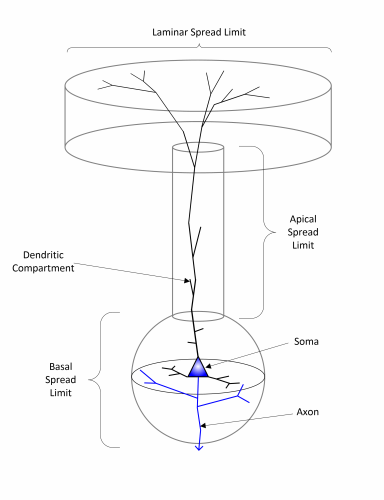
Below image shows the SpikeFun v0.90 pydamidal cell:
Improved Precision of Simulation Build-Up
Introduction of new pyramidal cell model also mandated some improvements in the competitive cell growing algorithm. As it could be seen from the image above, each cell type has its own axonal and dendritic arbor spreading limits per layer. Essentially, those limits are cylindrical (except for the basal dendrites which have spherical spreading limits).
So, testing whether axonal and dendritic arbors of two canditate neurons overlap includes cylinder-cylinder intersection test. Unfortunately, cylinder-cylinder intersection test is computationally very expensive if it is to be solved numerically. Due to undesired complexity of cylinder-cylinder intersection testing, previous versions of DigiCortex engine were using the most popular approximation, widely used in 3D graphics applications and which treats cylinders as capsules. A capsule is bounded by two spheres which radii equal the cylinder radius. This way, overlap test becomes computationally trivial and consists of testing whether the distance between two line segments which represent cylinder axes is less than sum of the cylinder radii.
While computationally much more desirable, approximation of cylinders with capsules brings unwanted "false positives" if only spherical parts of capsules overlap. In our case, this would mean unwanted breaches of cortical layers, where connections should not exist.
Due to this reason, DigiCortex v0.90 implements full cylinder-cylinder intersection test once the capsule test is passed with positive result (capsules intersect). Instead of expensive numerical solution for cylinder intersection, DigiCortex implements Monte Carlo method, which consists of generating random points inside the source cylinder volume, transfoming those points so that target (test) cylinder is axis-aligned and finally performing inexpensive "point in axis-aligned cylinder" test. Added benefit of this method is that it also allows us to obtain the intersection volume which can be used for guidance of how many synaptic sites should be formed (this is not done yet).
All-in-all, Monte Carlo method is computationally attractive and can be implemented in the highly optimized way. For example, it is not necessary to generate random points more than once per cylinder basis, as the basis points can be just simply translated along the cylinder axis. This way, test requires small number of randomly generated points and simple matrix multiplication to get the points transformed appropriately. As the test terminates as soon as single intersecting point is found, in most cases it would terminate after just few steps.
Largest SpikeFun Simulation Ever - 3.52 Billion Synapses
Below video shows the largest ever SpikeFun simulation so far - with 16.7 million neurons and 3.52 billion synapses. Current version of DigiCortex has a limit of 4 billion synapses in total, so this simulation is pretty close to the current limit. Simulation required approx. 350 GB of memory - and took approx. 2 hours to initialize on the dual CPU Xeon E5-2687W system with 16 cores running @3.1 GHz each.
Interesting phenomenon that could be observed in the simulation is the build-up of activity clusters. Also, EEG (shown near the end of video) shows desynchronized activity across different cortical regions:
- Log in to post comments